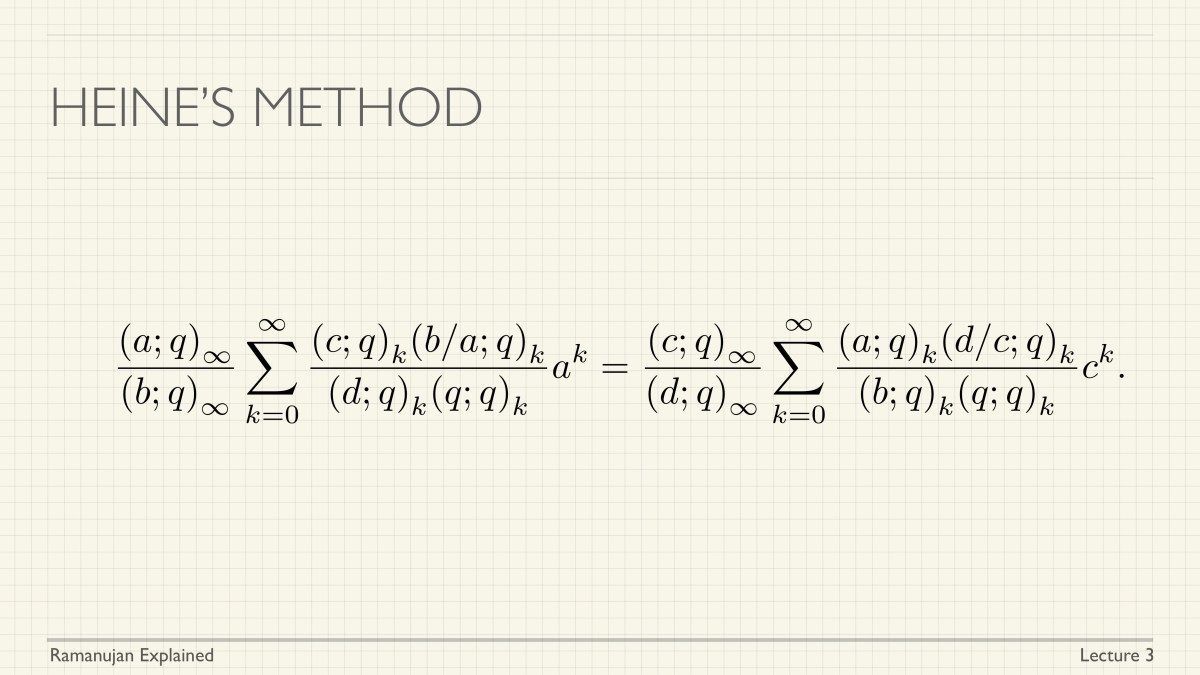Tag: III.16.2

Abstract

We explain what Andrews and Berndt call Heine’s method. This is a simple technique which gives many important and useful transformation formulas. The method is one used by Heine in what was the beginning of basic hypergeometric series, and this is one technique you need in your tool kit.  Of course, Ramanujan rediscovered the key results due to Heine, and found many more. This lecture (and exercises) will have many entries from Ramanujan’s Chapter 16, and from the Lost Notebook.  Andrews has suggested Heine’s method is behind the discovery of the famous mock theta functions—but that story we will tell another time.

Click to download slides

Viewers in China: please use this link (courtesy Shishuo Fu and group)

Link for live broadcast

Abstract

We begin our study of Ramanujan’s identities. The Rogers-Ramanujan identities appear Chapter 16 of Volume 3 of Berndt’s Ramanujan’s notebooks. One of the key results is the q-binomial theorem. We will begin with a discovery approach to the binomial theorem and then give Ramanujan’s own proof of the q-binomial theorem. Ramanujan developed hypergeometric series in an earlier chapter, so chances are that he was motivated to find a more general series with an additional parameter.

Click to download slides

Viewers in China: please use this link (courtesy Shishuo Fu and group)