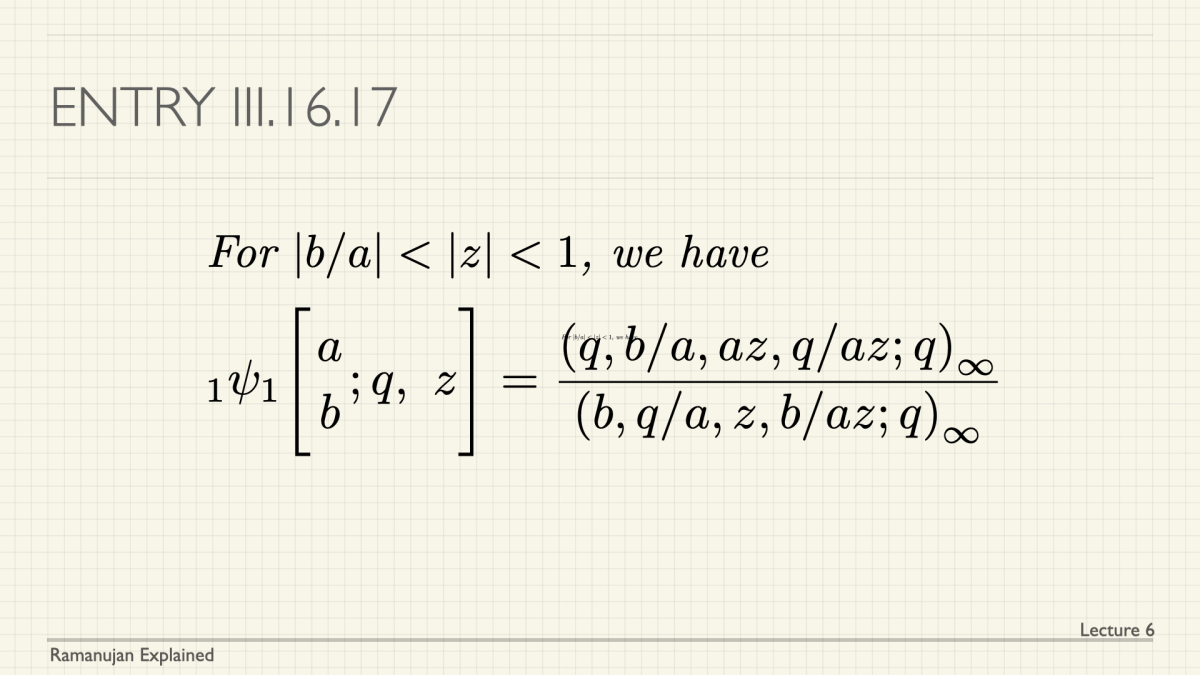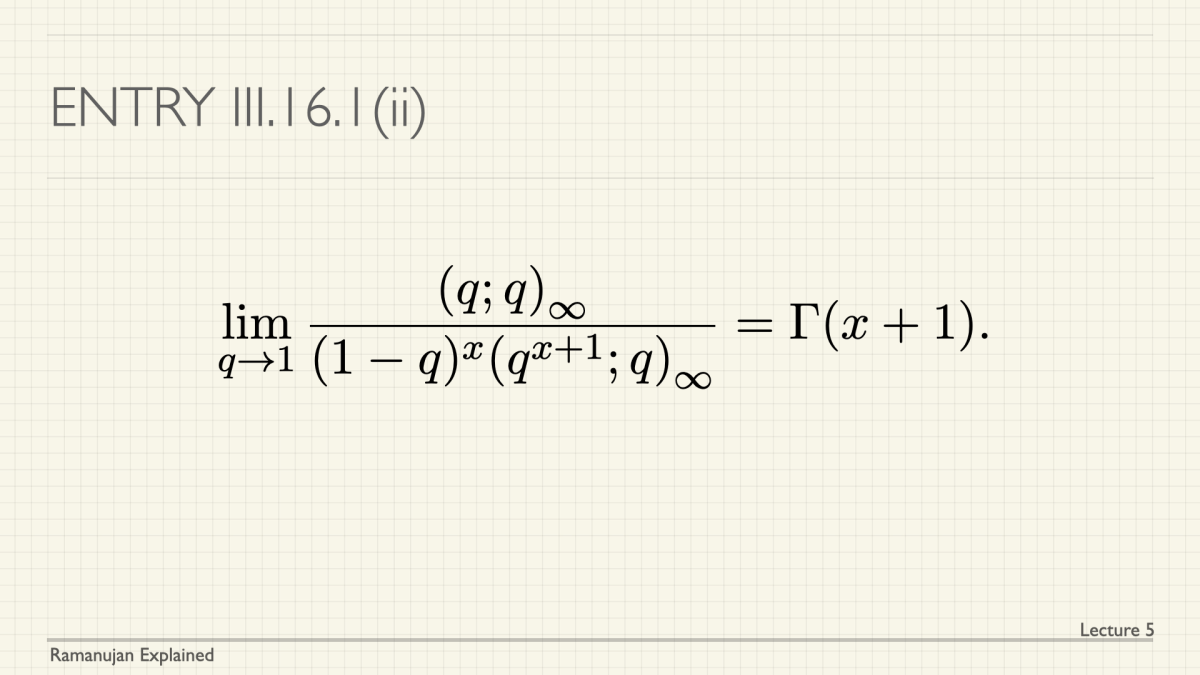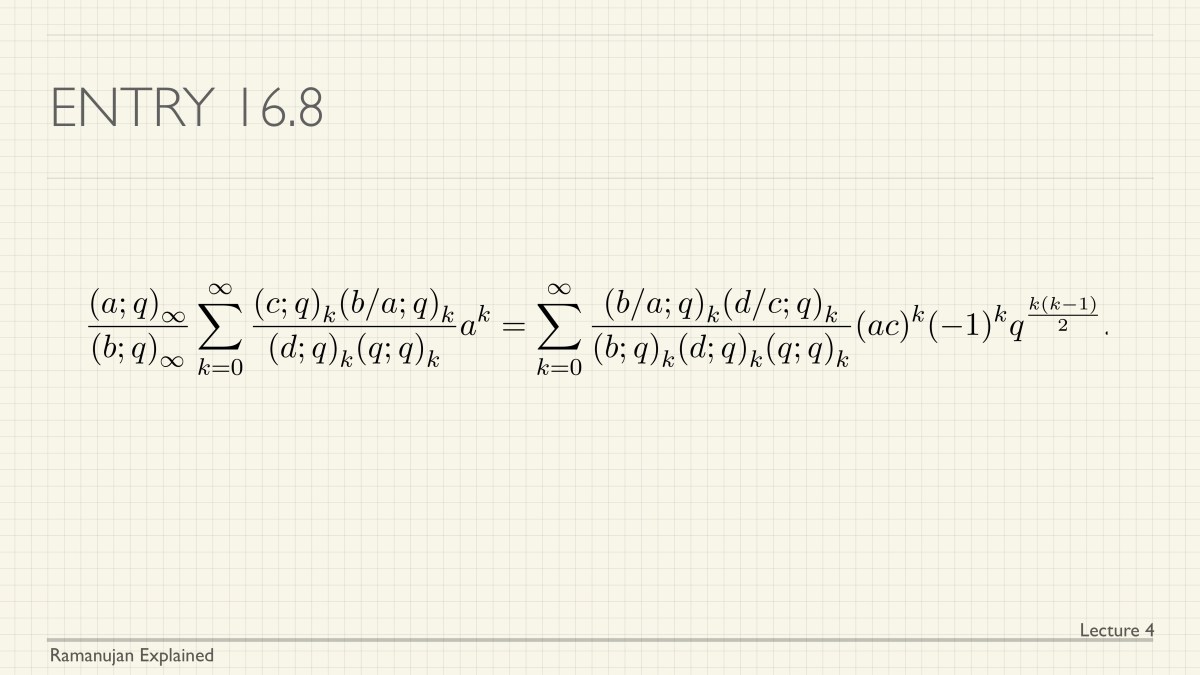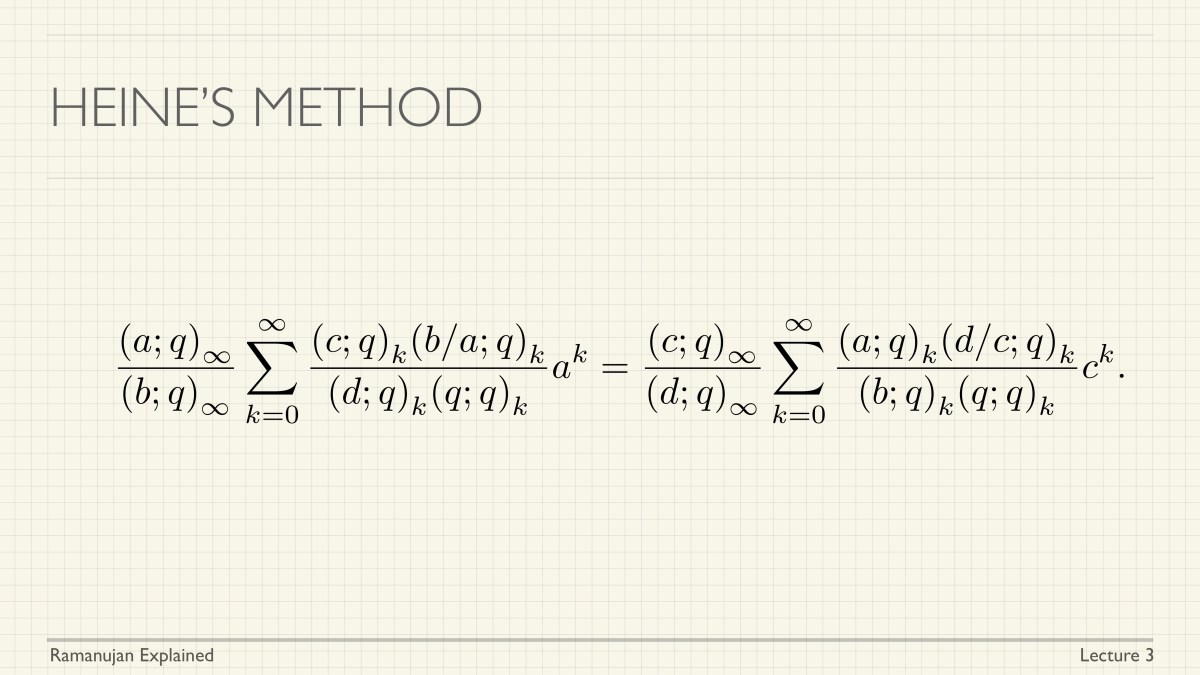Featured

About Ramanujan Explained

We have launched a course under the title of Ramanujan Explained. There will be a series of lectures, all given by Gaurav Bhatnagar, with accompanying notes and exercises. The goal is to cover (a large number of) Ramanujan’s identities. Please share this announcement with students who may be interested in Ramanujan and his mathematics.  

The first few lectures will target $q$-hypergeometric series and special cases, and can serve as an introduction to basic hypergeometric series. We hope these lectures will serve as a useful supplement to the monumental work of Bruce Berndt  (Ramanujan’s Notebooks I-V) and George Andrews and Bruce Berndt  (Ramanujan’s Lost Notebook I-V).

Lecture 2: The q-binomial theorem

Title: Ramanujan Explained 2: The q-binomial theorem

Speaker: Gaurav Bhatnagar (Ashoka University)

When: Thursday, May 2, 2024, 4:00 PM- 5:00 PM IST

Where: Zoom: Write to the organisers (sfandnt at gmail dot com) for the link

Link for live broadcast

Abstract

We begin our study of Ramanujan’s identities. The Rogers-Ramanujan identities appear Chapter 16 of Volume 3 of Berndt’s Ramanujan’s notebooks. One of the key results is the q-binomial theorem. We will begin with a discovery approach to the binomial theorem and then give Ramanujan’s own proof of the q-binomial theorem. Ramanujan developed hypergeometric series in an earlier chapter, so chances are that he was motivated to find a more general series with an additional parameter.

The following will be updated after May 2.

Click to download slides

Lecture 2. The q-binomial theorem

Viewers in China: please use this link (courtesy Shishuo Fu and group)

Lecture I: How to discover the Rogers-Ramanujan Identities

Title: Ramanujan Explained 1: How to discover the Rogers-Ramanujan identities

Speaker: Gaurav Bhatnagar (Ashoka University)

When: April 18, 2024, 4:00 PM- 5:00 PM IST

Where: Zoom: Write to the organisers (sfandnt at gmail dot com) for the link

Abstract

About the Rogers-Ramanujan identities, Hardy famously remarked: “It would be difficult to find more beautiful formulae than the “Rogers-Ramanujan” identities… ” In the first introductory lecture in the Ramanujan Explained course, we explain Askey’s idea on how Ramanujan may have come across these identities. Continued fractions played an important part of Ramanujan’s work, and Askey’s explanation is all about the simplest $q$-continued fraction and how it naturally leads to the Rogers-Ramanujan identities.

Click to download slides

Viewers in China: please use this link (courtesy Shishuo Fu and group)