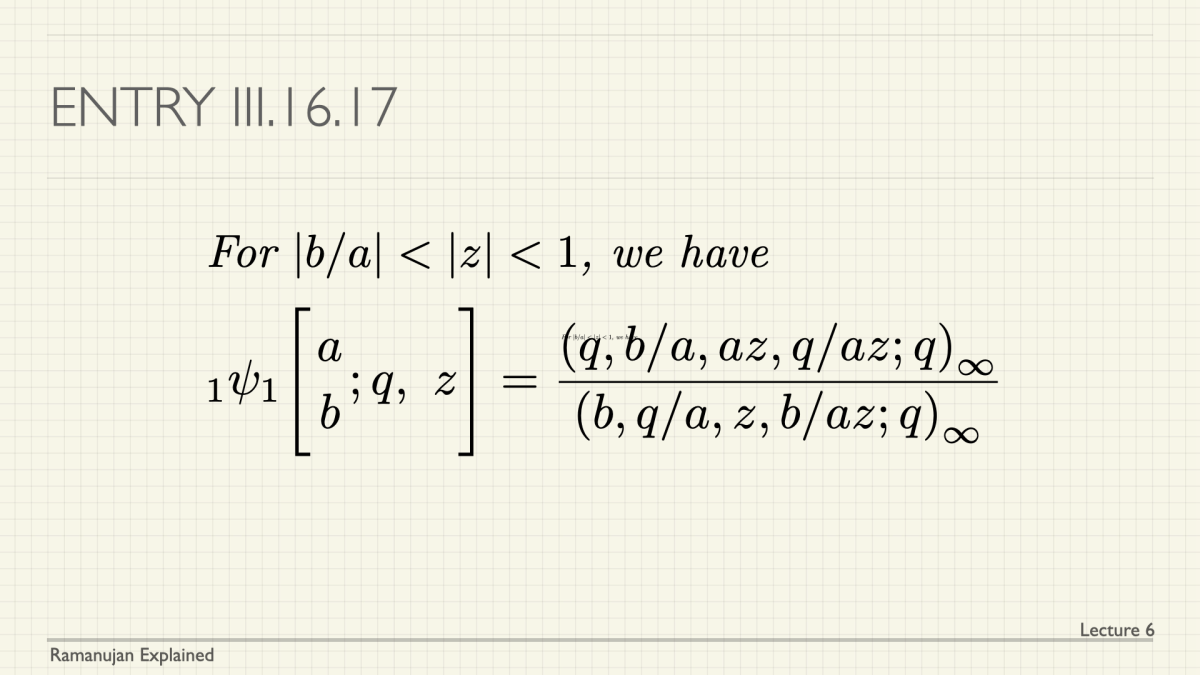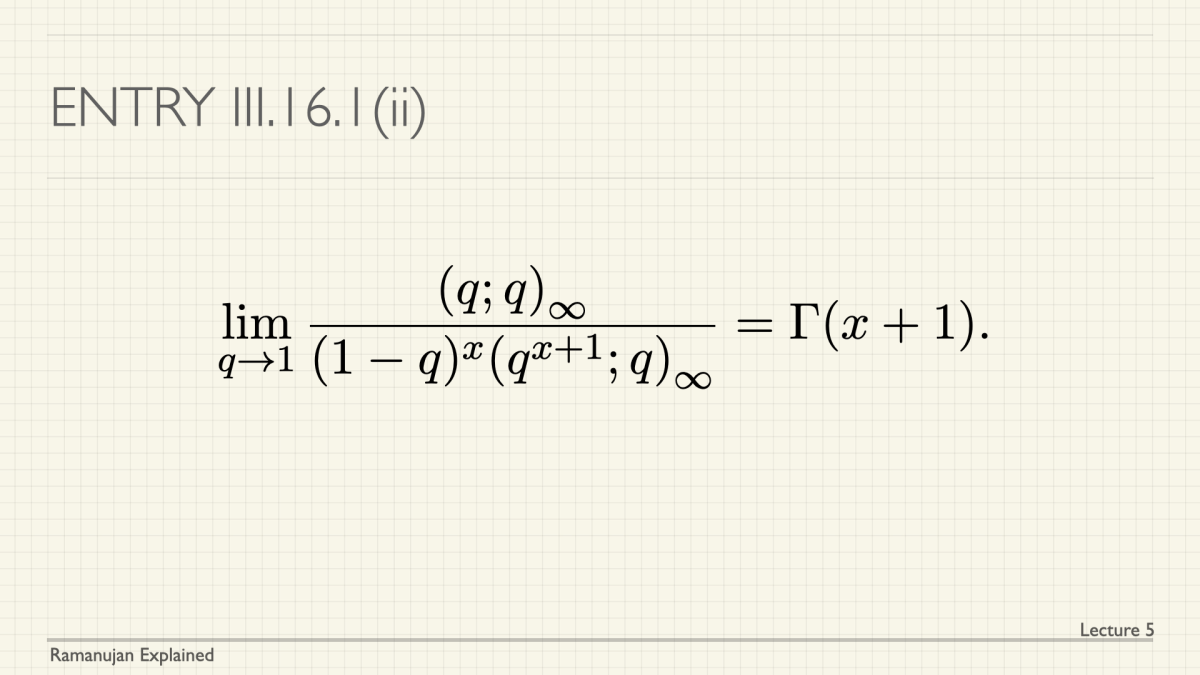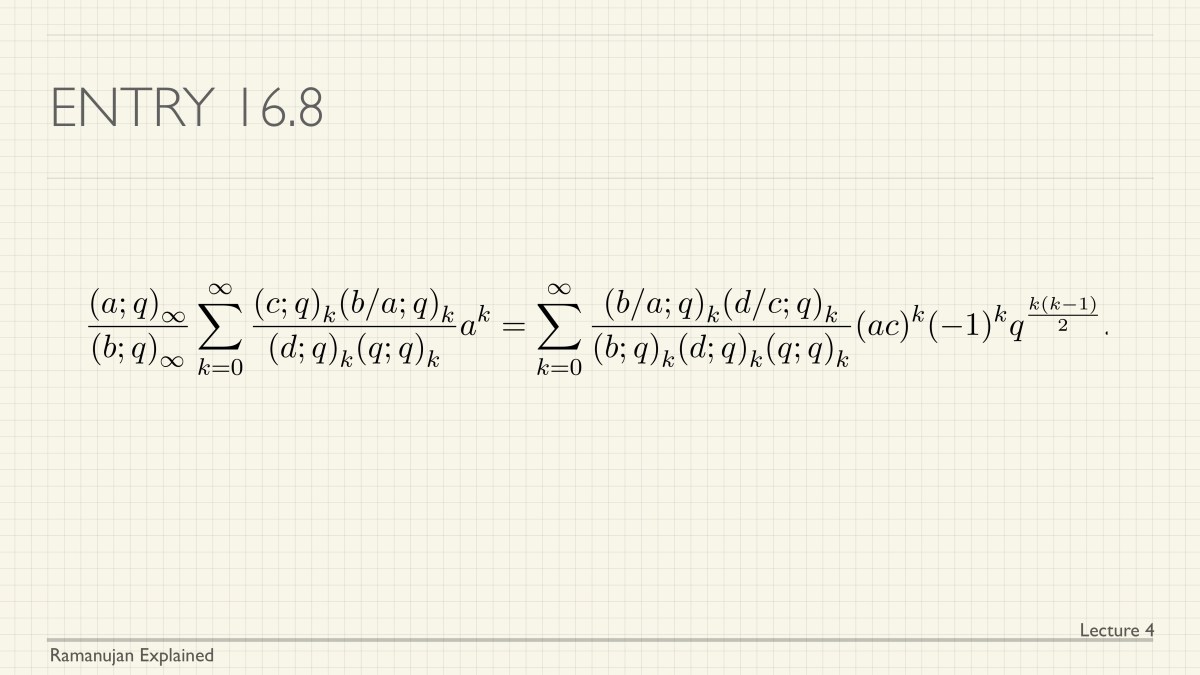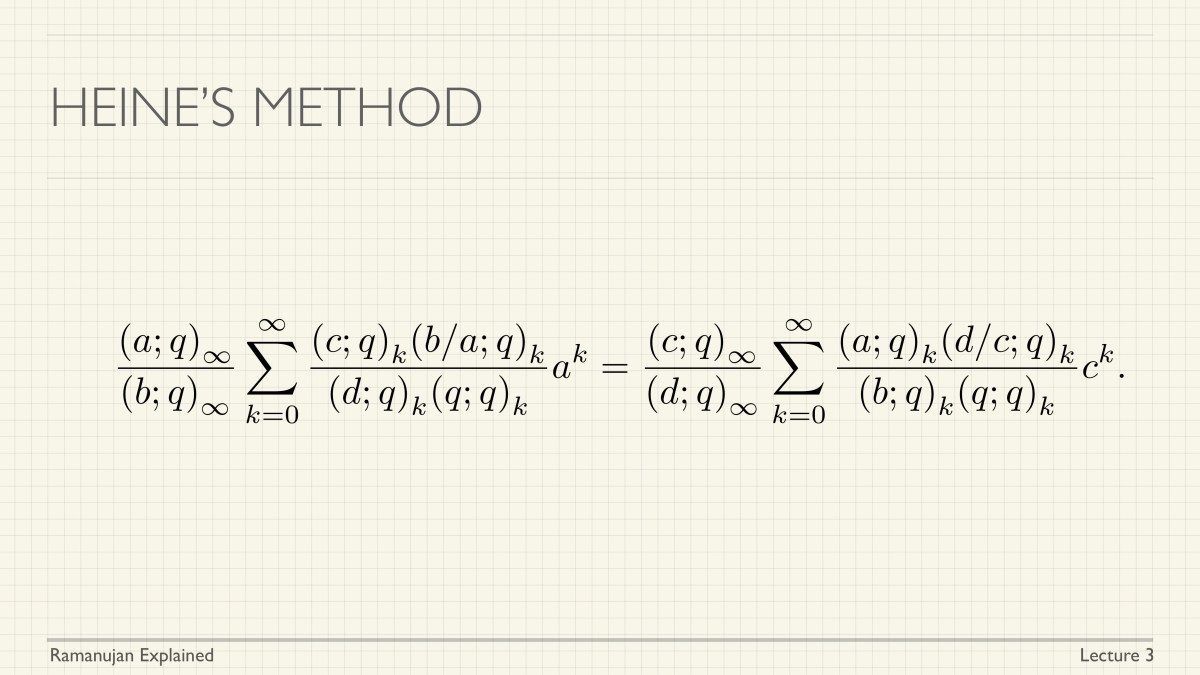Gaurav Bhatnagar

Lecture 6: Ramanujan’s 1-psi-1 sum

In the previous lecture in the series, we considered infinite products and the $q$-Gamma function. Now we consider an important product called the theta products, that were considered by Jacobi and are involved in his famous triple product identity. We obtain it as a special case of a result of Ramanujan.

I began including some of the background material, and I will continue with bits and pieces of that as we go along. This may mean somewhat haphazard development of the background material. But we want the focus to be on Ramanujan’s identities. So the background material is motivated by what is required to understand Ramanujan’s entries.

Talk Announcement:

Title: Ramanujan Explained 6: the $_1_\psi_1$ summation
Speaker: Gaurav Bhatnagar (Ashoka University)
When: Sept 26, 2024, 4:00 PM- 5:30 PM IST

Abstract:We give a proof of Ramanujan’s famous bilateral sum for a $_1\psi_1$ sum. The proof is Ismail’s celebrated proof. While it is the proof from `The Book’, it is not Ramanujan’s own proof. It contains Jacobi’s triple product identity and has many corollaries giving product forms of Ramanujan’s theta functions.

Click to download slides

Lecture 5: The q-Gamma Function

So far, we have covered 26 entries of Ramanujan. Talk 5 in the series Ramanujan Explained contains background material on infinite products. The idea in this is to cover some of the background material on infinite products so we can take limits of ratios of some infinite products and obtain hypergeometric special cases. This will help us rapidly increase the count of Ramanujan’s entries, and also help set us up for entries involving theta functions.

Title: Ramanujan Explained 5: The q-Gamma function

Speaker: Gaurav Bhatnagar (Ashoka University)

When: Thursday, July 25, 2024, 4:00 PM- 5:00 PM IST

Where: Zoom: Write to the organisers (sfandnt at gmail dot com) for the link

Abstract

We introduce infinite products and learn how to formally take limits of some ratios of infinite products. This is regarding the $q$-gamma function. Ramanujan had mentioned this limit in Entry 1 of Chapter 16 (Entry III.16.1(ii)) so it is a basic tool in his armoury.

Click to download slides

Lecture 4: Entry III.16.8

Title: Ramanujan Explained 4: Entry III.16.8

Speaker: Gaurav Bhatnagar (Ashoka University)

When: Thursday, June 27, 2024, 4:00 PM- 5:00 PM IST

Where: Zoom: Write to the organisers (sfandnt at gmail dot com) for the link

Abstract

We go over many transformation formulas from the Lost Notebook which can be obtained as special cases of the formulas obtained by using Heine’s method. These are to be included as exercises in our notes.
The main topic is another transformation formula that Ramanujan found useful. This is Entry III.16.8.
This is obtained by a minor modification of Heine’s method, and an example of what Wilf called the “Snake Oil Method”, given that it is used so often to prove identities.

Click to download slides

Lecture 4. Entry 111.16.8

Viewers in China: please use this link (courtesy Shishuo Fu and group)

Lecture 3: Heine’s Method

Title: Ramanujan Explained 3: Heine’s method

Speaker: Gaurav Bhatnagar (Ashoka University)

When: Thursday, May 23, 2024, 4:00 PM- 5:00 PM IST

Where: Zoom: Write to the organisers (sfandnt at gmail dot com) for the link

Abstract

We explain what Andrews and Berndt call Heine’s method. This is a simple technique which gives many important and useful transformation formulas. The method is one used by Heine in what was the beginning of basic hypergeometric series, and this is one technique you need in your tool kit. Of course, Ramanujan rediscovered the key results due to Heine, and found many more. This lecture (and exercises) will have many entries from Ramanujan’s Chapter 16, and from the Lost Notebook. Andrews has suggested Heine’s method is behind the discovery of the famous mock theta functions—but that story we will tell another time.

Click to download slides

Lecture 3.Heine’s Method

Viewers in China: please use this link (courtesy Shishuo Fu and group)

Lecture 2: The q-binomial theorem

Title: Ramanujan Explained 2: The q-binomial theorem

Speaker: Gaurav Bhatnagar (Ashoka University)

When: Thursday, May 2, 2024, 4:00 PM- 5:00 PM IST

Where: Zoom: Write to the organisers (sfandnt at gmail dot com) for the link

Link for live broadcast

Abstract

We begin our study of Ramanujan’s identities. The Rogers-Ramanujan identities appear Chapter 16 of Volume 3 of Berndt’s Ramanujan’s notebooks. One of the key results is the q-binomial theorem. We will begin with a discovery approach to the binomial theorem and then give Ramanujan’s own proof of the q-binomial theorem. Ramanujan developed hypergeometric series in an earlier chapter, so chances are that he was motivated to find a more general series with an additional parameter.

Click to download slides

Lecture 2. The q-binomial theorem

Viewers in China: please use this link (courtesy Shishuo Fu and group)

About Ramanujan Explained

We have launched a course under the title of Ramanujan Explained. There will be a series of lectures, all given by Gaurav Bhatnagar, with accompanying notes and exercises. The goal is to cover (a large number of) Ramanujan’s identities. Please share this announcement with students who may be interested in Ramanujan and his mathematics.

The first few lectures will target $q$-hypergeometric series and special cases, and can serve as an introduction to basic hypergeometric series. We hope these lectures will serve as a useful supplement to the monumental work of Bruce Berndt (Ramanujan’s Notebooks I-V) and George Andrews and Bruce Berndt (Ramanujan’s Lost Notebook I-V).

Lecture I: How to discover the Rogers-Ramanujan Identities

Title: Ramanujan Explained 1: How to discover the Rogers-Ramanujan identities

Speaker: Gaurav Bhatnagar (Ashoka University)

When: April 18, 2024, 4:00 PM- 5:00 PM IST

Where: Zoom: Write to the organisers (sfandnt at gmail dot com) for the link

Abstract

About the Rogers-Ramanujan identities, Hardy famously remarked: “It would be difficult to find more beautiful formulae than the “Rogers-Ramanujan” identities… ” In the first introductory lecture in the Ramanujan Explained course, we explain Askey’s idea on how Ramanujan may have come across these identities. Continued fractions played an important part of Ramanujan’s work, and Askey’s explanation is all about the simplest $q$-continued fraction and how it naturally leads to the Rogers-Ramanujan identities.

Click to download slides